wps怎么做双因素方差分析
粉丝904获赞6887
相关视频
 01:35查看AI文稿AI文稿
01:35查看AI文稿AI文稿excel 怎么做双因素方差分析?这是不同广告媒体上不同广告计划对应的销售额数据。现在我们想知道广告媒体和广告计划对销售额是否有影响?这就是一个方差分析的问题,用 excel 就可以轻松的搞定。在菜单数据中选择数据分析, 这里有两种,如果要考虑交互作用,就选择可重复双因素方差分析,否则选择无重复双因素方差分析,这里考虑交互作用,选择可重复的。确定 输入区域呢,选择这个区域,每一样本的行数呢是二。每一个广告媒体啊,对应两行数据, a 法呢,就是显著性水平。用默认的零点零五输出区域呢,我们让它显示在表格的下方, 确定得到方差分析的结果。上方呢是广告媒体和广告计划对应的观测数求和均值,方差,下方呢,是方差分析的结果。我们重点看这里的 p 值。第一个行因素,也就是广告媒体 对应的 p 值大于零点零五,说明广告媒体对销售额呢,没有显著性的影响。第二个列因素,广告计划 p 值小于零点零五,说明广告计划对销售额有显著性的影响。第三个交互作用, p 值也是大于零点零五,说明交互作用对销售额呢没有显著性的影响。这就是用 excel 做可重复双因素防查分析。
231孙斌说数据 00:54查看AI文稿AI文稿
00:54查看AI文稿AI文稿一分钟学会用 excel 做防查分析,这是品牌,这是地区,中间的表示销量。想知道品牌和地区对销量是否有显著性影响,在菜单数据里找到数据分析, 找到方查分析,无重复双因素方查分析,输入区域,选择上方的数据区域,勾选标志显出性水平,又默认的零点零五输出,选择输出区域,让结果显示在下方,确定给书方查分析结果。 第一部分是描述性统计分析,给出了品牌和地区的求和均值和方差。第二部分才是我们要关心的 行因素,也就是品牌 p 值非常小,小于零点零五说明品牌对销量没有影响。另因素也就是地区 p 值大于零点零五,说明地区对销量有显著性的影响。这就是用 excel 做防杀分析。
2639孙斌说数据 03:34查看AI文稿AI文稿
03:34查看AI文稿AI文稿哈喽,大家好,今天给大家讲一个预测数据的新方法,就是数据分析里面的指数平滑。那之前给大家讲过一个预测数据的方法,那是首先我们选出数据, 然后我们数据里面的预测工作表,那我们可以选择预测结束时间,比如说选择最晚三十号, 还有我们选择一个周的,那我们选项里面最新期间,那我们可以自己调啊,越大那他这个范围越大,那越小范围就越小,那我们点击创建的话,他就会把上限值和下限值都会出现,那我们这 种方法是比较笼统啊,那我们今天讲的数据就比较细啊,预测的数据就比较细致,那今天讲的数据,首先我们点中数据,然后我们在数据分析里面的指数平滑啊,点击确定,那我们 输入区域就是我们的 b 二到 b 十一,那我们阻尼系数,阻尼系数这里呢?那前提是如果我们的数据波动性 越大,那阻尼系数就越大,那波动性越小,那阻尼系数就越小。标志的话就是我们如果选中销售额点标志我们不选,不选中的话就不用点,我们不用管,那我们今天分别选三个稳定系数,我们首先 算零点二的,那输出去,输出去,我们点 c 二,那我们确定, 然后我们点零点六的指数平滑,我们把它改成零点六,然后我们点第二我们点确定, 然后我们点数据分析里面的指数平滑,那么改零点九,然后我们点一二,我们做个对比, 那如果我们要算十一号的值,那我们如果选选择算十一号的值,那么他都拉下来,一个 拉下来,然后我们都就进行了预测啊,比如说如果是十号销售了, 实际销售了幺零九九五,那我们他会预测十二号,十一号销售的是幺零六二九,那用第二个总结数数预 预测他销售幺零六二九,那零点六的销售额就预测他销售万零六,那零点九的总计销售就有效销售,预测他 销售的是八千八百九十六,那我们如何预测到十二号呢?那如果我们的是一号,销售的是一万块,那我们再把它下拉一个,那我们零点二的促进去注意预测,看销售 一万零一百二十五,那零点六预测他销售的是一万零四啊,相对来说零点和零点六相对准确一点,零点九相对来说误差比较大,因为我们的 原数据它波动性不是特别大,所以我们零点二的到零点六之间的总结系数是合理的,那就是这样预测,那我们实际执意输入,那我们可以在 再次再预测他的下一个值啊,就这样预测啊。今天讲的这个预测方法,大家学会了没啊?学会了,麻烦大家点个关注加双击,谢谢!
155小李飞叨 10:32查看AI文稿AI文稿
10:32查看AI文稿AI文稿当你的变量内形里面有一些是分类变量的时候,特别是你要探索两个两个分内变量之间 是一个什么样的关系,或者是两个分裂变量与另外一个连续性的变量是一个什么样的关系。这个时候呢,我们就可以用到下面的这些方法, 主要是交叉表分析、卡方分析和这个方叉分析。其实方叉分析在呃各个领域,在在生物学啊,在这个心理学啊,都运用的还是非常非常广泛的,所以说呃方叉分析也是非常重要的一个重要的一个分析方法。 那么方向分析的,其实有时候我们也把它叫做 f 检验,也是把它叫 f 检验,它在本质上呢,实际上是比较两个或者两个以上的样本均值是否存在显著的差异。 虽然他叫方差分析,他本质上比较的是两个和两个样本之间的均值,因为跟均值相对应的还有一个是方差,对吧?而且他在分析的过程是御用的一些方差,所以我们把它叫做这个方差分析,他本质上是比较几个样本之间的这个均值。那么我们说方差分析的目的就是实现梳理出 各个不同的这个分类变量。分类变量就说我们质变量是一个分类变量,然后阴变量呢,可能是一个这个呃数值性的变量, 我们要看不同的这个分类变量对一些事物是否具有显著性的影响,特别是连续性的变量是否具有显著的影响。比如说我们这个里面用的分类变量,用性别,用不同广告的类型,都是我们所说的这个分类变量,对吧?那么 呃连续性面料或者我们所说这个数字性面料有什么呢?比如说这个用户对于产品的购买意愿,用户对于产品的购买意愿, 对吧?这个都是我们所说的这个连续性的这个变量。呃,连续性的变量或者是数值性的变量。好,它的原理是什么呢?它原理呢?实际上就是说利用主内及主间这个偏差平方与自由度,呃计算出主内主间的这个军方的这个值,从而计算出 f 值, 然后依靠这个 f 分布去判断呃变量之间的这个关系是否存在变量之间是否存在显著的这个差异。说的相对来说有一点偏专业哈,相对来说偏专业。但是如果你完全没有学过统计学,也没有学过概念论,你就理解一点,就是不同组织他的均值是不是一样的? 方才分析就是要做这个不同组建的均值是不是一样的,但是为了从统计上判断他的均值是不是一样的,他可能他运用了一些其他的一些指标,比如说主内组建的这个军方,呃,这个军方的这个值啊等等等等一些其他的那些 判断。那么从操作上呢?显著差异是否是等于显著影响?是的,我们说显著差异就是说他的他 a 对 b 的影响,他 他存在显示他就说 a 对 b 的影响,他不是等于零,他是大于零或者是小于零的,所以说 a 对 b 就有显著的影响。好吧,那么方叉分析他有一些要求。要求呢?首先是这个质变量和这个音面量之间的这个关,呃,这个类型是有要求的, 首先是要要求分析分类变量与数值性变量这样的关系,我们刚才已经给大家强调过了。第二个呢,就是说他对样本的要求,他是两组或者多组之间 数据之间的差异进行呃进行检验。就像如果我们进行这个,如果只有两组的话,他在本质上他实际上也是一种 t 检验,是本质上也是一种 t 检验,对吧?我们说 f 检验和 t 检验他本身是有一个关系的,本身是有一个关系的。也是这里其实也是可以反 根据自备量的这个类型,我们可以把方差分析分为单一组方差分析、双一组方差分析和这个多一组的方差分析。当然这个分类其实跟我们前面讲这个,呃,回归分析的是我分类方式,实际上是有一些类似的哈,有一些类似的 回归分析的时候,我们有一元现金回归和这个多元现金回归,对吧?然后这里呢,我们有单因素分叉分析和双因素分析分析,还有多因素分叉分析。 呃,我们这里面在进行分析的时候,都是说质变量是一个或者是多个,但应变量肯定是只有一个的。在统计分析里面,如果应变量有多个的情况下,有多个的情况下,也可能会存在,也可能会存在。但是这种呢,比较复杂,比较复杂,不建议那种基础不是很好的同学去使用。 如果基础不是很好的话,你就去做一些比较常规的分析,比如说这个回归分析啊,方向分析也是我们今天要讲的这一些目,主要 目的哈,就采用一些比较简单的方法去得出你们需要的结论,而不是说上来就会说,我会,会,我会很多分析方法,我来把我所会的分析方法全部来一套,那没有这个必要,没有这个必要。 好,那么方叉飞机怎么去操作?呃,首先呢,我们要去计算这个方叉飞机的这个主内方叉和主尖方叉,然后通过主内方叉和主尖方叉呢得出这个 f 值,根据 f 值去查对应的借零借表 临界表,确定这个临界表的这个值。然后呢去根据我们的这个呃 f 值和临界表的这个值 进行比较,然后以及去看去判断,如果 f 值是小于零戒值的话,一般就说明他的 p 值肯定就是大于零点零五了,一般就说明他们之间是没有显著差异的。 如果 f 值大于零借值, f 值比零借值大,然后就说明变量之间存在显著的差异,也就是说这个分类变量对我们这里所说的这个数字变量是有显著的影响的。呃,有同学问到说方拆分析、卡方检验都是大于零借值的时候显著,对吗? 实际上啊,不管是方差分析还是卡方卡方分析,还是我们所说的回归分析,他都是一样的。就是说你根据你算出来这个 f 值或者是这个 t 值去跟你的这个零界值进行比较,当你的 f 值 t 值越大大于零界值的时候,那么你的 t 值是会越小的,这个是我们说是存在显著差异的。 如果你的 f 值 t 值或者是 p, 呃,或者是这个卡方值他都是小于你的零戒值的话,一般他的这个 p 值就会大于零点一五,就说明没有显著的差异,这是我们从原理上,从原理上进行了这个 讲解。那么从操作上呢?操作上一样的,我们还是按照我们之前的这个思路,从操作上给大家讲一下。从操作上我们在分期数据或者收集数据的时候呢,我们有两类变量,一类是分类变量,也是我们所说的质变量,对不对?分类变量或者质变量, 我们呢就可以去啊,把这个质变量放到这个分析分析的这个质变量方框里面去。然后呢?呃,因变量呢?可能是连续性的变量,可以是购买意愿或也可以是信息性,或者这个趣味性。假设我们看这个购买意愿, 我们就会发现这个性别,这里面性别呢,就说女性对这个购买医院的均值是五点三二三五,男性的是五点一九三九,对吧?这个值好像是有差别,因为从这个数值上看,女性的这个值是比男性的这个值大的,但这个值从统计上 是不是一定是女性的这个购买医院比男性的统计医院大?我们需要去做这个方差分析,做这个方差分析,我们读出来这个 f 值是多少呢? f 值是零点四五八七, 零点四五八七,零点四五八七,得出来这个 p 值呢?可能就是呃,因为这个值已经比较小了哈,已经比较小了,一般你至少要呃大于,一般要大于二或者大于三嘛,这才会显著。好,那么在这个零点四五八七的这个情况,你的 p 值就会 大于零点零,我们说这个影响是不显著的,影响是不显著的,那么影响是不显著,有可能是什么?有可能是 因为你分析的时候,你的这个样本的这个样本的这个男女比例不协调,对吧?有可能是你这个分析的比例不协调,或者是什么样子,要去找一下原因。所以说我们在分析的时候哈,一般是一般是这个样子的,我们在收集数据的时候再给 给大家强调一下,分析的时候呢,为了平衡,为了平衡这个性别啊,平衡这个地域,一开始的时候,你不要一开始就比如说我要收集一千二百分问卷,或者我会收集收集四百分问卷,我一开始咔就把四百分问卷给设置了。 你如果这样设计的话,首先你的这个人力成本和这个人力物力财力就发挥很大的,这个人力物力财力,结果一收起来发现啊,要么你们问,就你们有一项有问题, 问题里面有一项有问题,那么你需又需要全部重新推到全部重来,这个对你来说是有很大的损失。 所以我们建议,我们建议大家在做的时候呢,做的时候做这个,呃,做一次前侧,做一次前侧,也就是在正式发布问卷的时候,你做一次前侧,前侧就是在发布之前测一下你这个问卷,测一下你的这个收集收集数据的 方式是不是合理的收据收据是不是合理的,如果不是,你可以稍微进行修改,这里的损失也只是少部分。我们说 t 检验是可以,但是 t 检验,因为我们说 t 检验是 f 检验的一种,对不对?不是说 t 检验不是 f 检验,他只是一种,这实际上是我们所说的单因素方差分区,不是说他不是方差分析,好吧? 如果是有多个变量的话,那么你就需要做什么?如果有多个变量,你就需要把多个变量放在一起做这个方差分析就是多因素方差分析。多因素方差分析呢?可能还会有一个,呃,可能还会有一个更复杂的情况,就会出现这种交叉,就是交互的影响。 就比如说这一个是性别,那么一个是性别,一个是年龄,那么性别和年龄他们除了这个性别会对这个购买意愿产生影响,年龄会对购买意愿产生影响,那么他们才会有一个交互。就比如说男性在年 的时候是什么样子,女性在年轻人什么样子,这个时候就会有一个交互影响,那么交互影响的他这个 他这个分析方法。呃,我们在后面可能会讲到这个是我们对于这个方差分析的一个基本的这个讲解。当然我们也可以分析这个不同年龄对这个购买医院的对不同年龄对购买医院的影响,不同年龄对购买医院的影响。这个时候呢?呃, 我们就会发现不同年龄层呢,他的购买意愿是存在这个显著差异的,因为 p 值是等于 f 值是大于三的,大于三,而且 p 值是小于零点零五的, p 值是小于零点零五的,对吧?这个时候我们就说年龄对消费者的购买意愿存在显著的差异 啊。有同学问到,就是说啊,刚刚讲的这个交互影响是不是属于双因素分析?呃,双因素一般就是说我们讲双因素区别于单因素,就是说你的影响因子啊,是有两个,就是你的分 那边呢?是其实是有两个,对不对?但是交互交互影响是说这两个背量之间,这两个背量之间是存在相互的这个影响的,好吧?在后面的时候呢,呃,后面的章节里面老师会讲到如何去做这个调节效应。调节效应的分析在这里只是给大家简单的提一下,就是, 呃,你在做这个双因素分析的时候,或者多元呃,分析的时候,你要注意到可能会有这个调节效应,就是我们所说的交互效应。
 00:42查看AI文稿AI文稿
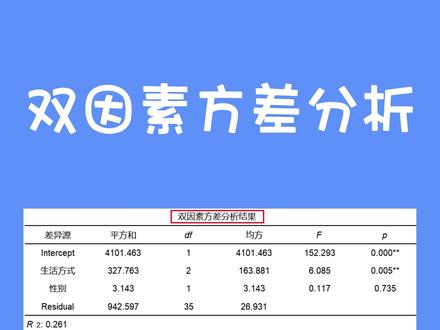
00:42查看AI文稿AI文稿双因素方差分析看这个就会了。双因素方差分析用于分析两个定类数据与定量数据之间的关系情况,例如,研究不同性别生活方式对于减重效果的差异情况。在 so 系统中选择双因素方差分析, 拖赚样本至相应分析框中,点击开始分析双因素方差分析结果,从上表可知,生活方式呈现出显著性, 性别没有呈现出显著性。生活方式会对减重产生差异关系,而性别不会,你学会了吗?
185SPSSAU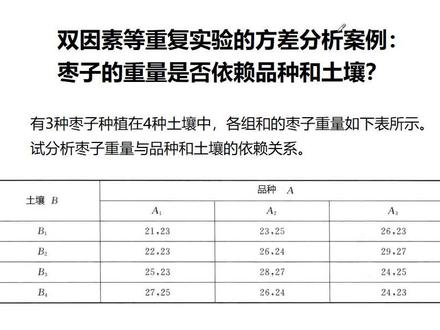 13:03查看AI文稿AI文稿
13:03查看AI文稿AI文稿枣子的重量是否依赖于这个品种和土壤?那我们这里考虑这个等重复这个情况下的方法分析, 这个时候我们要考虑这个品种和土壤的这个相互的作用,所以这样的情况下呢,这个这里品种是三种啊, 土壤是四种,所以我们等会把这个记号改成,这边改成 a, 这边改成 b 啊,为了和后面的这个保持一致,这每一种组合它这里啊产生了两个字,这相当于是这个枣子的在两块这样的地上的一个平均值,可以这样去理解。 下面我们先看一下这个双因素翻杀分析的一个简略的介绍。在这个教材里面呢,在 等重复之下,那么这个 a 因素,比如说你分了二种水平, b 因素分了这个 s 种啊,然后每一个组合里面又进行了这个 t 字实验, 这里就有三个数啊, st, 所以这个总数就是这三个相乘, 就是全部的 x 的数量,就 rs, t 相乘,对吧?这个 x 可以认为他们服从正态分布,因为这个正态分布是各种因素叠加之后的一个效果。根据大数地,根据中心经验定理啊, 这个可以写成这个样子,这个 miu ij, 然后这个一个零君子的正态风格,对吧?然后呢,这个 miu 呢,是全体的君子, 这个缪 i 一点呢,就是按韩的君子,没有一点接,那就是按列的君子,这个阿法埃北塔接就是 d i, 韩的君子的偏差 d, 接列的君子的偏差相当于是 a 的那个水平的, a 的这个因素的影响和 b 的那个因素的影响,对吧? 好,然后呢,这个啊,这个 miu i 街呢,你可以写成这个样子,这你把这个阿尔法和贝塔带过来呢,这边剩下的就是这个相,所以两边是一样的, 所以那么这个啊,没有 ij 可以分成这四个,这个伽马相当于是这个水平 a i 和 b 接的这个交互的作用,相互的以这个交互影响好,到了这里以后呢,那么我们这个 x i、 j、 k 呢,可以表 导致这个这四个量 miu、 阿法、贝塔、伽马加上这个 epan i j、 k, epc 是一个林君子的这样的一个正态分布,那么这个阿法就代表了 a 因素的影响,贝塔就代表 b 因素的影响,伽马 ig 就是 a i b 接的这个相互的作用。 所以下面我们这个翻插检测呢,要考虑这三种假设问题。第一个是不是所有的阿法都是零,就说明 a 没什么作用, 这个所有的贝塔是不是等于零,就说明 b 这个因素也没什么影响,对这个结果。第三个角色就是所有的钢瓦是不是都等于零,所有的钢瓦都等于零,说明 a 和 b 之间呢,相互的作用一起可以忽略, 所以那么这里啊就考虑了这个相互作用啊,下面我 引进一些统计量,那么这个 x 一横呢,就是全体的均值,全部的 x 加起来除以总数,这个 x i 接一点的一横呢,就是对第三个分量求和以后平均,这个 x i 点点一横就是对后面两个下标求和平均 x 点接点一横呢,就是对第一个和第三个下标求和再平均。好,那么这个 s t 就是全变差呢?总变差呢,就是你这个 x i、 j、 k 这个任何一个项和你这个总君子的这个偏差,总偏差程度,是吧? 这个总偏差了,你可以分开,可以分开成这样的啊,四个像这里,那么这个这个像和这个像可以抵下, 这个像和这个像抵消,这个像和这个像抵消。这里捡了两个 x, 总体君子里加了一个,是吧?和这里完全一样,是吧?这样一打开了就变成四个平方,和那些交叉相全部都变成零了, 好,那么这四个项呢?就分别是这个,这是总的这个平方叉变变叉,是吧? s 一, s, a, s, b, s, a 和 b 啊, s 一相当于是一种误差, s a 就是 a 的那个因素的影响, b 因素的影响,然后呢,这个 a 和 b 的这个交交叉的影响,对吧? 那么来分析他的自由度啊,那么你总共的这个 s t 呢?就是显然就是因为他这里减了一个样本君子,所以他是总数 rst 减一,减掉一个自由度,因为它是减了一个君子啊,好,那么其他的这这四个项的这个总的自由度应该和他是一样的,那么这个 sa 呢? 写上这里是加了二个项,他减掉一个样板君子,减少一个自由度,这里是加了 s 个项,减掉一个君子呢,也损失掉一个自由度。好,那这里呢?啊,这个 这里也减掉了一个这样的这个 rs 啊,然后这个 t 减一,因为这里就是对 t 求和的时候呢,他要损失掉一个自由度, 那所以啊,所以这个这个呢,这里减掉了两个菌子 啊,这个顾算要稍微复杂一些啊,这里你可以用总数来减一下,最后你可以得到呢,就是总数 rst 减一啊,这是总的自由度,减掉这三个以后,剩下他的自由度呢?就是啊,减一 s 减一这么多个自由度啊。 好,那么这个呃,可以去计算一下他们的这个期望值, 变成标准叉,这个翻叉以后,再算他有七万值的这个 s 一呢,这个除以这个叉的自由度以后呢?就是这个,就是那个那个那个翻叉。 好,那么这个 s a 这个变成标准差以后呢?这里他可能还有一个这样的像,所以这个在 h 零一成立的情况下,就是所有的阿法都等于零的情况下,这项就没有了,对吧?这样的话,他们一比呢, 这个像两两个像一比,这个比那个呢,就会产生一个这个 f 分布,这个地方也有一个这样的像,如果这些贝塔 都等于零的话,那么这项也没了,那么这个他比上他也会产生一个 f, 这里有一个这样的平方上, 所以在这个 h 零,这个这个阿法都等于零的下情况下,这个 fa 呢?这两个比一下就是一个这样的 f 分部,那么可以构造他的这个拒绝欲呢,就是 f 足够大, 因为他这个分子啊,可能会多一个这样的下,他会,如果他大的太厉害的话,就就应该拒绝了,对吧? 就不是这个 h 零成立的情况,那么这个 fb 也是一样构造这个啊,那个统计量以及他的这个拒绝率 fa a 叉 b 呢,这个也是一个这样的 f 分布,他这里也多了一个这样的项链,所以他的拒绝率的构造都都是一样的。 好,那么这里把这个总结了一下,这个因素 a 因素 b 交互作用以及这个误差相,这是他们的自由度啊, 这几个加起来就是这个,总之有度。然后呢,这个画上均标,这个翻插以后呢,删除一下就变成 fa、 fbfa、 叉 b 这个三个检验统计量。 现在回到我们刚才那个例子啊,一开始这个例子对,我们把它记为 a, 这里记为 b 啊, 我们用 max 来不来看一下这个推算啊?那么这是 数据啊,带进去之后呢,这个,这是第一第一组啊,这是第二组,我们要用一个三位数组,然后呢把这个啊 fa 算出来呢,是二点四三, 这个 xa 这个拒绝预示三点四,比他小的吧,说明 a 这个因素影响不大,影响不那么显著。 fb 是四点多,然后他的拒绝预示三点八, 这个比他大了,所以 b 这个因素影响比较显著。这个 f a, b 是四点二,他的那个啊,这个拒绝率的下线是二点九,所以也比他大,所以对我们这个例子来说呢,就是 a 这个因素影响不大,就是土壤啊, 土壤影响不显著,但是品种影响是显著的,他们的交互影响也是显著的。 交互影响呢,你可以看到这里是二十七,是比较大的,但是这里又变成二十四了,对吧?所以这个土壤呢,对于不同的品种他也是有不同的情况,但是这里呢,同样的品种他有二十九,对吧?所以土壤和品种之间他有一个相互的这个作用。 像我们再看一个例子啊, 比如说呢,这个一个火箭 用四种燃料和三种推进剂做射程实验,那么这个是燃料,有四种,这个推进剂有三次,推进器有三个 构成,一十二种情况,对吧?这个是 r 等于四, s 等于三,然后这个 t 等于二,每一组都做了两 两个实验,对吧?发射火箭两次啊,下面我们要问这个推进剂和燃料两因素对射程有无显著的影响, 然后把这些算一下,之后呢?这个什么 stsasbsa 叉 bs, 一算完以后,最后把这个 f 都算出来, f a, f b, f, a 乘 b 啊,四九一十四啊,这这些数,再去查一下这个, 这应该是零点九五啊,这个都应该是零点九五, 都比这个要大,所以这个 a 水平呢?不同燃料对射程有显著影响,这个 fb 也是大于这个 啊,进到了这个拒绝玉里面去了呢,所以在这个不同的推推进剂也是有显著影响, a x b 呢,这个也是大于这个啊,也进到进去拒绝玉里面去了,所以这个推进剂和燃料的交互作用也是显著的,而且还可以提高到零点九九九。 他这里应该是啊,因为 f 分布是这么个情况, 就你这里是 f, 应该是零点九五啊,这个概率才是零点零五,对吧?这里是接受,这边是零点九五。 好,呃,这样, 而且我们可以看出来,从那个表里面可以看出, a 四和 b, a 三和 b 二,这个搭配,是啊,最好的一种搭配, 对吧?你看 a 四和 b 一,这里都达到了七十多啊, a 三和 b 二,这都达到了七十多,对不对?其他的远远超过其他的组合啊。上面来用 metal level 来核对一下啊, 那么这是那些数据,我们这也用一个三维数组, 三位数组来表示,因为他也每每一组每一个组合做了两次嘛,相当于是放在两页纸上,是吧? 然后呢,我们把这个 fa 算出来四点四,他的这个拒绝率是三点四,所以也被这个拒进到这个拒绝域里面去了。 fb 是九点多,他的这个拒绝于三点八也进去了,对吧? fab 一十四,然后这个是二点九,所以 啊,这个交互影响也进去了。第二个这个情况是八点多就把那个自信水平提高了以后呢?八点多,但是这个意思是还是比八点多要大,所以呢,这个啊,就是燃料和推进器对这个火箭的射程都有显著的影响 这么一个情况。那么这个是双因素反差分析的一个两个简单的例子啊。
88胡天山 02:37查看AI文稿AI文稿
02:37查看AI文稿AI文稿大家好,欢迎来到观看优斯学院的视频,记得先点赞再关注我们。今天我将会为大家介绍如何使用常用的 excel 办公软件来进行 innova 检验。 正如我们在课程中提到, a nova 检验可以用于比较两个或多个组之间的均值是否存在显着的差异。 a nova 检验的方法是将总方差分解为组内方差和组间方差,通过比较组间方差与组内方差的比值来判断组别的均值是否存在显着差异。 优斯学院认为大部分的六锡格马统计工具都可以透过 excel 完成,而不必要一定使用 mini tap。 以下我将会介绍一下如何利用 excel 进行方差分析。首先单击顶部 excel 菜单中的数据 data, 然后再分析部分,查找数据,分析 data analysis。 如果您没有看到 data analysis, 你就可能需要另外去安装它了。 现在我们把三组数据输入进来进行比较,我们会选择分析功能表单中的 a nova 单一因子这个功能来执行这个检验。然后在 input 下选择所有数据列的范围,在分组方式中选择列 column。 如果第一行中有有意义的变量标签,例如 a, b, c, 请选中标签复选框 labels in the first row。 这样做的话输出结 果实会更清晰。另外, excel 使用默认的 alpha 值,零点零五也是我们最常用的值。最后单击 ok, excel 就会输出结果。 最后一步就是分析输出的结果。在方叉分析表中,我们可以看到 p 值是零点一二二五四三八, 这个数值并不小于我们设定的显着性水平零点零五。所以我们不能推翻原假设,意思就是我们的样本数据未能掌握足够有力的证据来得出三个总体均值不相等的结论。 如果你想更深入了解各种质量管理和不同的数据分析工具,可以学习六西格玛绿带或者黑带,也可以关注我们优斯学院的视频,我们会每天为你提供各种各样相关的小知识。
42优思学院六西格玛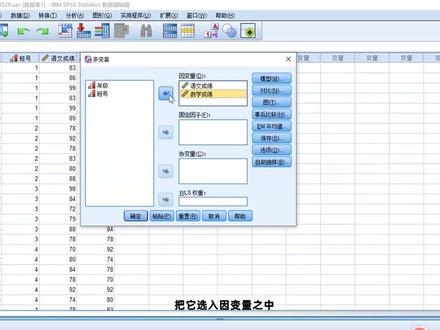 06:04查看AI文稿AI文稿
06:04查看AI文稿AI文稿大家好,这里是 fpss 学堂,我是主讲人斯洛。本节的内容为两因素多元方差分析, 我将从两部分出发,一是方差分析的统计条件,具体讲解两因素多元方差分析的含义以及方差分析的案例。 第二部分为方差分析的具体统计操作。那么什么是两因素多元方差分析呢? 所谓的两因素多元放差分析是用于研究多个音变量是否受两个字变量也成为因素的影响, 他检验的是两个因素取值水平的不同组合之间因变量的均值是否存在显著的差异。那么两因素多元方差分析该怎么做?我们一起来学习一下。 我们来看一个案例,不同的年级和班级对语文成绩和数学成绩是否有显著影响呢?那在这个问题中,我们不难发现有两个字变量,分别是年级和 单别音面量为语文成绩和数学成绩。那在这个里面就是一个典型的两因素多元 帮他分析。那么我们一起来看一看在 spss 中的具体操作。 首先我们打开数据集,在这个里面有四列数字,分别是年级、班号,语文成绩和数学成绩。那么我们来操作一下。首先单击菜单栏中的分析, 选择一般线性模型,然后选择多变量,打开多变量对话框, 然后我们的音变量是语文成绩和数学成绩,把它选入音变量之中,然后我们的字变量为年级和班号,把它选入 固定因子当中。然后这个操作和我们之前的操作大同小异,模型这里我们选择默认值就可以了, 对比这里面我们还是选择默认值即可,然后事后比较,这里我们还是默认值,重点在 em 平均值。那在这个里面我们把年级选过去, 单号选过去,他们的交互选过去,然后勾选比较主效应,然后单击继续 保存,这里面呢我们勾微标准化就可以了。选项描述统计,习性检验,笑容量 估算,然后单击继续,在完成一项操作之后,我们点击确定按钮,输出结果即可。 首先是主体键因子,在这个里面我们不难发现一共有六个年级单号,有四个,每个里面的个案数都已经清晰的列出了。 那么第二个描述统计,描述统计在这里面我们不做坠数,都是对于每个年级不同班号进行的一个平均值以及标准差的检验。 然后这个里面我们看一下写放差举论的同性检验,那在这个里面我们可以看到显著性是零点七四二,大于 零点零五。 接下来我们看一下多边料检验这个表格, 那在这个里面我们看一下年级他的显著性是零点二零一,单号他的显著性是零点五六七, 年级和八号之间的交务效应,这里面是零点四三三,这三个值呢都是大于零点 零五的啊,都是大于零点零五的,所以我们可以推断年级效应,八号效应和年级乘八号效应对模型的影响是不显著的。 最后最重要的表格就是主体间效应检验, 在这个里面表格显示的是各效应检验的输出结果。那么不难发现,从各项显著性的检验的批值我们可以看出, 年级单号对语文和数学成绩的影响并不显著,这个里面我们可以看到年级 他的显著性是零点七一七,大于零点零五,单号显著性零点三零一大于零点零五,对吧?这个是语文的,那数学的同理都在这里, 年级的是零点零五零啊,这个班号的是零点七四六啊,同样的也是大于零点零五,他们的交互也是大于零点零五,所以我们就可以推断出我们的年级班号对语文和数学成 的影响并不显著。 以上就是本期内容,更多 spss 知识请关注 icpss 学堂微信公众号。
341SPSS学堂 00:49
00:49 00:37查看AI文稿AI文稿
00:37查看AI文稿AI文稿双因素方差分析结果怎么看?首先分别分析两个 x 是否呈现出显著性,如果呈现出显著性,说明 x 不同组别会对外产生显著性差异。以下方分析结果表格为例,对于 x 而言, f 等于十一点五七二, p 等于零点零零一、零点零五,呈现出显著性, 说明主效应存在, x 会对外产生差异关系。对于 xr 而言, ap 等于零点八六零, p 等于零点四二三、零点零五,没有呈现出显著性, 说明 x 二并不会对外产生差异关系。如果二阶效应显著,且前提是存在一阶主效应,可继续通过表格和图形研究二阶效应情况。你学会了吗?如有其他疑问,请在评论区告诉我。
95SPSSAU 07:41查看AI文稿AI文稿
07:41查看AI文稿AI文稿大家好,那么今天的话呢,来给大家讲一下大家在一些文献当中所看到的这种表格的一个制作方法哈,然后呢,呃,然后以及在哪些方法可以用到这样的一个表格哈?首先的话呢,像这一类的这种加减 有数值的这种表格,首先我们得知道它代表什么啊?那么一般这类的表格会出现在方差分析里面,包括努力样本 t、 配对样本 t 以及单因素方差、 多因素方差。而我们这一篇文献里面,他其实做的就是一个多因素方差的哈,只不过他分成了两个表。那么,呃,一般做差异分析里面涉及到这些方法都可以整理成这个样子啊,可以整理成这个样子,这个其实很简单哈,因为我们在做差异分析的时候,都通常会输出一个 均值和标准差,对不对?所以这个表里面的这个数值,前面这个数值代表的是它的得分,这个分组在某一个变量上的一个得分,一般是均值或者是总分哈,一般是均值或者总分,然后后面这个加减号,后面这个是一个标准叉, s d 标准差, 然后这个加减符号,它只是代表的是一个起到一个呃中间的一个作用,并不是代表的说,哎,二点三,三加零点三或者减零点三,他不是一个范围值啊,他只是起到了一个连接的作用,连接的作用不代表说加减这个数值,知道吧?所以呢,呃, 这样去整理的一个目的呢?第一呢,是为了把表长很长的一个表格,或者是说,呃,很多我们不需要的一个指标呢,我们就把它忽略掉,然后只保留一些重要的指标,那么就是我们的得分 和标准差,然后呢下面就是一般是 f 值呀, t 值呀,显著性 t 值,对不对?那么这个呢就是我们的呃一个表格的一个来源,那么一般就是出现在差异分析里面哈,差异分析里面,那比如说我们今天要讲的这个这个案例哈,这个案例呢?是 啊,比如说我们要比较性别在购买意愿上的一个差异,那么购买意愿它是由题目去组成的,然后计算出来的一个总分或者是平均值,那么这里是一个平均值啊,那现在的话呢,我们要去做我们的一个独立样本体检验,因为 我们的性别是二分类选项啊,二分类选项。然后呢做参数检验里面的独立样本机,配对样本机以及我们的单因素以及多因素方差,都要求我们的音变量,或者说不同分组的的音变量的数值,他的一个正,这个什么呢?趋势呈现一个正态性的一个结果。那么一般来说的话,问卷数据,只要他的数据偏 态不是很严重的话,我们都可以用参数检验的方法啊。那么我们直接点分析,然后呢比较均值里面的独立样本期,然后呢我们把呃性别放进去啊,性别放到分组变量里面,然后定义他一般是两个组嘛,所以你就是他二十七点零以后的,他都会自动跟你生成这个值, 然后呢继续就行了。然后这里需要强调一点,因为有一些文献他已经开始去呃去显示我们的,去展示我们的一个效应大小了,那么这个效应大小在二十六点零以下及以下的版本都没有这个功能哈,就二十七、 二十八会有这样的一个功能,所以呢,如果要做效应估估算哪个效应大小呢?尽量用二十七或者是二十八点零去做啊,然后这样去做完了之后,你确定就行了,得到的一个结果呢?就是这样。那么得到的结果呢?怎么去整理呢?我们先把小数点给他, 给他省略一下哈,我们需要多少位小数,我们就保留多少位小数哈,然后像标准叉啊,看见没有?标准叉在这里,标准叉在这里,然后一般三位小数就行了 啊,或者是两位小数都可以。那么这个呢,就是我们所需要的那个加减的前面那个数值和后面那个数值,我们先把这个复制出去,呃,复制出去哈,好,我们放大一点。另外一个也需要 啊,还有最后一个消音值的哈。那么一一般的话呢,我们需要干什么呢?把这个弄成这样的表格怎么弄呢啊?要在 excel 里面去做哈,在 excel 里面去做。首先一个,我们要是第一步先插入我们的符号,找到正符号,那个符号一般在这里找不到,或者在更多里面去找。 然后呢,输入输入一个加减,看见没有他就出来了,加减两个字他就出来了,然后先插在这里,然后我们先复制他,用水 c 复制他,然后在这里输入函数等于什么呢?等于平均值这个单元格。然后呢,输入英文状态下的这个符号,再输入双引号, 双引号里面放什么呢?放加减号,起到一个连接的作用,然后再输入一次这个连接符号,然后再点标准叉,然后回车他就出来了哈,回车他就出来了,然后这个呢就是 操作方法啊,然后呢?嗯,这个就做好了,做好了之后呢,我们就需要把这个整理一下,对不对啊?一般整理的话呢,整理成这样,请别啊, 因为我一般我们做差异分析的时候不可能只做一题嘛,他人口学变量会有很多啊,性别啊,年龄啊,对不对?所以呢这个呢我们就可以这样,呃, 点亮点亮。然后呢这里就是购买意愿,购买意愿得分,或者有些他会表示成什么呢?有些他会表示成 这种,就是大写的 m 加减 s d 的,或者是这里它有的时候它会 s d 会表示成 x 上面有一根横线的。这种啊,这个是标准叉哈 啊,这两种都可以的,然后把这两个值给他复制下来啊,给他复制下来啊,这个就是他的一个得分,然后一般还需要放什么呢?放 g 值和 p 值对不对?那么这里的话呢,像前面这些什么 f 值那些都不重要,自由度呢,可以不放,然后后面这些可以不放,所以呢我们只用什么呢? p 值 和 p 值好,还有一些效应量哈,效应量如果要放的话就放 消音量,就是怎么放呢啊?写个消音量就行了,消音量啊,然后这个呢就是一个表格了,那么表格的整理的话呢,你看梯值用哪一个呢?我们就直接判断这里方差小一点点,零五方差不相等,所以我们用下面这个梯值啊,那下面这个梯值,然后梯值是什么呢?梯值他很小对不对?不是零号,他只是接近零, 所以一般表示为小于零点零零一效应量的话呢,独立样本 t 的,我们看这个值就行了,点估计一点一点九一九八 一九八哈,然后这个呢,就是我们的一个独立样本期检验的一个表格的一个整理哈,就是这样的了哈。然后呢?呃,像他的这种呢, 为什么他不把批值啊放在这里?因为他这里做的是一个多因素方差哈,他涉及到一个交互,涉及到一个交互,所以他用了两个表去表示啊,那两个表去表示,那当然的话,一般,嗯,涉及不到多因素的话,只是单因素和独立样本 t 的话呢,一般这样就行了。比如说,呃,你还要去做年龄的,对吧?年龄的单因素方差,那么一样的,这里面你再输入一个斜杠 f, 那就是说说明是 t 值或者是 f 值嘛?那做独立样本 t 呢,他当然就是 t 值了哈,做 f 做单因素方差的话,他就是 f 值哈,那一样的单因素方差,他是也是一样的结果。 比如说我们做年龄的年龄,它有很多个选项,所以呢,我们选单数和魔法检验,然后把这里弄成年龄就行了。确定,然后呢,你会发现这里同样是有平均值和标准差的啊,我们就用这两列来作为加减的这种这种形式用刚才那个方法,然后呢取 f 值和 p 值, 然后如果有是有这个有差异的,我们进一步的去看多重比较的结果,然后呢,放一偏一塔方,这里看的是偏一塔方哈。所以呢,为什么我们刚才那里用的是一个效应量的值,而不是直接把这个放进来,因为不利亚本 t 和我们的方差分析,单数方差分析他的效应量的值 指标类型不一样,所以呢我们直接写一个消音量,然后写下来就行了。啊,那么这种呢是就是我们类似于我们这种表格的一个整理啊。那么今天的内容呢?呃,就是分享到这里。
851根号三 04:06查看AI文稿AI文稿
04:06查看AI文稿AI文稿多因素方差分析用于分析两个以上的自变量对一面量的影响,要求自变量为离散变量, 音变量为连续变量。主要分析主效应、交互作用、单独效应三个方面。多因素放大分析最简单的形式就是双音速放差分析,只有两个字,变量和一个音变量。我们来看这个案例。 不同剂量运动对静坐、少动、中年女性血脂的影响,我们招募一批受试者, 随机分成四个组,每组六十人,分别为三十分钟中等强度组、三十分钟大强度组,六十分钟中等强度组、六十分钟大强度组。 这就形成了两个自便量,一个是运动时间,一个是运动强度,也就形成了二、 二吸音设计。吸音设计的统计分析方法通常是多因素方差分析,四个组在运动干预之后,分别测试受试者的血脂。二乘二吸音设计有两个次变量, 所以采用双音速放差分析。我们来看一下测试的数据,测试运动时间、 运动强度、两个次变量,这是血脂的四个指标,最后一个是低密度脂蛋白,对于高血脂人群,低密度脂蛋白属于低油指标,就是这个脂越小越好。 双音速方差分析的操作,点击分析一般线性模型,单电量、 运动时间和运动强度选入固定因子,低密度脂蛋白选入音变量。 通常点击选项勾选描述统计,会呈现出均值、标准差等基本信息, 还有骑行检验、效应量估计、实测密也是经常勾选的一些选项,我们后面再进行介绍,点击继续。通常结合图来分析结果,所以点击图,运动时间选入水平轴,运动强度选入单独的线条, 点击添加,可以绘制交互图继续确定。我们来看一下结果, 这个是各组的均值标准差样本量在论文里可以做三线表,最重要的结果是方差分析的结果。运动时间和运动强度这两行都是主效应,运动时间成运动强度 是交互作用,主效应指的是单个自便量对于面量的影响,那么运动时间对低密度脂蛋白的影响,我们可以看这个皮值是零点二五六, 因为 p 值大于零点零五,所以主效应不显著。运动强度的主效应 p 值等于零点三零三,也是大于零点零五, 所以运动强度的主效应也不显著。也就是说单独考虑运动时间和运动强度的时候,都不会对低密度脂蛋白产生影响。但是运动时间和运动强度的交互作用显著,体脂等于零点零四四,小于零点零五。交互作用是什么呢?就是一个自便量对一面量的影响, 在另一个或多个自变量不同水平上的表现不同,一般表现为线图交互。我们结合图形来分析,交互作用 显著时,在线图里最明显的表现就是两根线有明显的交叉,或者说延长线有明显的交叉,可以这样来描述交互作用。当每天运动三十分钟时, 中等强度与大强度的差值明显大于每天运动六十分钟时候的他们两个的差值。因为低密度脂蛋白属于低油指标,越小越好。那么根据交互图我们就可以初步的判断结果。每天进行三十分钟的大强度运动, 或者说每天进行六十分钟的中等强度运动,能够有效的降低低密度脂蛋白 双因素放大分析或多因素放大分析,结果的情况会有很多种,我们今天只是介绍了其中的一种,后面会继续分享。
693科研与统计 23:43查看AI文稿AI文稿
23:43查看AI文稿AI文稿大家好,欢迎来到 spot 课堂,我是李博士,接下来我跟大家分享的是 spot 装音速重复测量包装分析及简单效益分析。 好,首先我们来了解一下装音速方章分析。呃,装音素,呃重复测量方章分析呢,主要是由,首先我们来看这装音素,装音素呢,一个音素呢主要是 不同总别也就不同处理,然后第二个因素呢,时间,这就是他的两个不同因素。然后呢还有一个交互交易,就是总别乘以时间,这呢就是他的一个交互交易, 然后针对某一个样板进行不同时间点的一个测量呢,呃,就是形成了一个 重复测量的一个数据,这样呢我们就需要进行呃双因素重复测量方差分析。呃,当我们做完双因素重复测量方差分析呃 之后呢,我们如果发现呃交互教育简著的时候呢,我们就需要进行简单教育分析,如果交交互教育不简著呢,我们就只需要看他的组别和时间的主教育就可以了。 呃,进行简单教育分析呢,有这两种方法,第一种方法呢就是分别来做 呃独立样本基点,如果是两根分组的话呢,对不同时间点的变量进行独立样本基点念或者单因素方章分期。呃,这是一块, 然后再一块呢就是,呃对数据进行拆分,就是对他不同组别对数据呢进行拆分,然后进行呢重复测量方向分解,这是一种。然后第二种呢,就是我们通过编解语法来实现,因为 spss 没有直接提供简单效应分析的一个呃操作内容,所以呢我们可以用这两种方法来实现, 关于重双因素重复测量方针分析呢,还是在我们上次课讲的内容里面的。呃,重复测量里面进行操作,然后呢直接重复测量,这个因子都是一样的,大家如果感兴趣呢,可以呃 按上次的内,然后这一块呢就是重复测量的主对话框,主体间因子,这里呢就需要选择上主别了,然后呢,呃,一个主体内呢,就是 不同时间点的一个指标的一个数值,主体间呢就是组别,然后重复测量呢,我们可以选择描述土地和其余点线的结果。 好,我们通过一个案例来看一下这个不同组别下三个时间点 这个指标呢是否存在差异,我们呢就需要做一下双因素重复测量方章分期。好,我们来打开这个数据看一下 分期,一般建议模型重复,车辆重置一下,这是时间,这是三 定义。呃,三个时间点的测量选进来,然后组别呢?主体连接选项呢,我们选上描述统计继续, 然后模型呢?这默认对比呢,我们也可以默认图呢,我们可以选择上水平轴呢是时间,单独的线条呢是指叠添加。师傅比较呢,我们可以不用管, 然后交平均值呢,这三个选项比较主要,光复蓝泥法继续。呃,保存呢,我们不用管,继续。确定。 好,我们来看一下他这个结果。呃,重点呢,首先呢我们来看一下他这个,呃 ad 来看一下吧。 呃主体内因子,这三个主体间因子个案处,这个都不重要,重点呢是我们看描述统计,这后面呢我们需要用到他这个均值标准差,然后多变量检验呢?如果不满足均匀度检验呢,我们 就叫来看多变量检验这组结果。好,这里呢重点来看求硬度检验,他呢是零点零五二大于零点零五,说明呢满足求硬度检验。 所以呢,主体内效应呢,我们是选择第一行假设求精度检验,这是 f 值,然后交互效应, f 值呢指是他,呃,就说明时间的效应是呃 具有统计学意义的时间和组别的主教育,交互教育呢,也是具有统计学意义的。然后再来看主体间, 主体间组别呢,这 f 呢是二十三点九八四,呃,说明这主体间呢,呃,也是有统计学意义的,然后再往下看, 再往下看呢,主角三遍量减,这是呃三个时间点加整体的一个差异,这个呢是他的一个统计量,然后整体呢是有差异的,然后时间呢, 这笔来轨迹呢,也是整体上是有差异的。然后第三块呢,就是给出来了一个实验组对应的一个 均值和标准差之他的一个描述,但是并没有呢给出他的一个差异性情况。所以呢,这里呢就需要进行简单教育分析了。 简单教育分析呢,我们还是根据刚才介绍的两块内容分别来做一下,第一 各哪方就是看一下方法捏, 就是独立样板体检验,呃,加重复测量方差分期这种方法来做 好独立样板体检验。就说呢,我们对通过独立样板体检验看 t 零 t e t 二有没有差异好分析。 组别组别呢,这里呢是一和二, 这是他的一个简单效应,呃下呢,就踢零时刻呢,呃,两组有没有差异?踢零呢,也没有 差异,第一呢有差异,第二呢有差异,然后呢我们再对数据进行拆分,就实验组下三个时间点与差异对照组下三个时间点与差异,数据拆分 比较足,然后呢再进行一次重复测量,防撞焊机, 这里呢就没有别了,刚才呢我们进行了选择,这里直接确定就可以了, 因为呢我们需要把有一些选项呢去掉,看一下哪些需要去掉, 重置一角, 然后选项 logo 统计 e m 平均值,选上时间,教主教育帮助了你一些, 确定好,这是数据拆分下的一个呃,对数据进行了拆分,分别做实验组和对照组下的一个重复测量,方差分期。我们我们来看这样组呢,第一组不满足方差几率,所以用到 是我们需要用格林豪斯盖斯勒这个 f 和 p 值。然后第二组呢是对照组呢,满足体型减量,所以呢用时间下的主效应呢,是用这个假设强度减量的结果, f 和 p 值也是就减除差异, 至于他是怎么有差异的,我们就看这个,这两两比较结果,一二三有差异,二一三二和三。实验组二和三是没有差异的, 对照组呢一二三有差异,二三呢这样是有差异的,这呢就完成了一个简单效应的分析,然后呢这是方法一,方法二呢简单一些,我们只需要添加两个代码就可以了, 我们来做一个,呃,添加代码呢,我们需要首先呢,他先让他生成一段基本的代码, 然后还是呢刚才把我们的操作都先操作一下,组别选项呢,保存描述成绩 平均值呢,这三个都选上比较主角与帮助了,你图呢,时间是组成组别呢,单独的金条添加继续粘贴 好,这样呢,形成了一组基,基础在哪呢?我们再进行添加两组,就是对这组下呢进行一个呢是进行时间,一个是进行组别, 这样呢,我们就通过添加这两行代码呢,进行了一下简单教育的分析,然后运行这一段代码就可以了, 你看这是我们的完整代码,呃,这是他的一个基本描述,然后呢,哦,刚才因为我们这是对数据进 进行了拆分,所以呢,我们对数据进行还原一下,数据拆分根据所有个案确定,然后呢,我们再重新运行代码就可以了。 好,你看我们现在呢是进行了完输出了完整的结果,这呢是一个主体内主体编译,然后描述统计,这是我们做表格需要用的数据。然后呢, 呃,酒精度碱面呢是零点零五二,说明呢是满足酒精度碱面的,所以呢,我们是按第一行结果,呃,时间主效 f 值, p 值,呃,时间组别交互效应的 f 值, p 值,然后组别的 f 值和 p 值,我们看到呢,交互效应是潜固的,所以呢,我们进行简单效应分析,简单效应分析是在 你看第三个,第三个是实验组下的一个不同之间点比较,这 呃错了哈,刚才应该是呃三呢是呃不同时间点下两个组别的比较对应着 f 值和 p 值,你看时间点击呢,就是七零 两组没有显著差异,是他皮值,然后时间点二和三呢,对于 f 值和皮值有显著差异。 然后这第四个呢就是对应的是呃实验组下不同时间点的两两比较结果,对照组下两两比较的结果,对应的,你看实验组对应的 f 值和 p 值, f 值和 p 值,这样呢就通过写写上这么两行代码呢,就可以实现呃专业组方章分析的简单教育分析了。然后关于制表呢,我们再来看, 我们可以做成这种形式,你看观察组,对照组,然后不同之间就是类似这样一种表格,我们来做一下, 先找到它的一个输出结果,这是均值, 均值呢,我们就一般写成均值加减标准叉的形式,所以呢直接写个繁数。呃,保留两个角度, 大家要注意,要解这括号的时候呢,其实需要在英文 pro 下 包括这符号, 均值加减标准差有了,所以呃实验我们来筛选一下,把这总记去掉, 然后这是 t 零,然后这是 t 一。 好,然后呢我们再 再来把它的一个检验结果写成把样板量都是二十五 简单效应的统计量, f 值和 p 值。 好,我们先来把它的一个呃主效应以及简单效应的一个以及交互效应结果选上。 f 时间等 时间主效应呢,它是因为满足精英度简便的,所以是按照假设精英度简便是它 f 之大 五三七,然后 p 值呢? p 时间呢,它是小于零点零一, 我们再来把这几个隔壁, 然后呢再来看 看组别的 f 值和 p 值, 他呢是在这里主别主体间教育简历。 然后呢再写时间和组别的交互效应, 它的数值呢是在这满足亲密度减九点 三七二, 负值呢, p 值呢是点零零零,然后时间点零零二, 这样呢,我们把它的一个主效应以及交互效应结果,这是主效应时间三六二点五三七等于零点零一, p 值阻别呢, 是他二十三点九八次小于零点零一笔值,然后这呢就是下标了, 好用格式刷一刷 w, 时间成组别成时间, 这样呢,我们把它的一个 主要结果给写上了,然后呢,因为他这交互效应显著呢,所以我们在需要进行他的一个简单效应分析。简单效应分析呢,就是分别对实验总价三个时间点有差异,对照总价三个时间点有差异,在 根据最后一次这个结果来,这是实验总价三个时间点五差异,这是 f 值对于 p 值, f 值对于 p 值对照值, 然后皮值呢,就是小于零点零一, 就是对应这儿的粘固性了, 然后 p 值呢,也是它两两比较呢,是否有差异呢?我们可以看到这一二三有差异,二跟三是没有差异的,所以我们用字母标注呢,就是这样, 呃,从大米标注的是 a, 然后二三是没有查 a、 b、 p 的 啊,关于字母标注呢,可以参考啊,前面发的视频就是,呃,跟单因素方案分析里面的一个字母标注法是一样的,因为二三没有差异,就是 abb 了,这个呢就是一二三有差异,二三有差异就是 ab, see you, 从大到小标呢 a, 然后这就是 b, 就是 c, 就说明呢, 呃,这对照组呢,三个点是有差异的,实验组呢?实验组呢,这个 t 一跟 t 二是没有差异的,也就说二三没有差异,然后分别在不同时间点下呢,呃,有位差异呢, f 值和 p 值我们对应过来, 因为是两组呢,所以我们就不用进行原来比较了, 因为他保留单位角度是零点零零零嘛,也就是说都是角于零点零零一,所以直接复制过来就行。 好,这是呢最完整的一个表格了,就是我们这里呢,包含了他的一个主效应交互效应啊,以及简单效应分析的结果啊。简单效应分析之后呢,又包含了两两比较的一个结果, 然后呢再进行一下稍微的格式调整,这样的结果呢就非常完整了。好,关于双因素包装分期呢,呃,就 介绍到这里,大家如果有疑问啊,再联系我们吧,因为这一块内容呢非常非常复杂,你看他这个方法呢,其实是一样的,就是在这表述一块呢,是稍微有差异 啊,大家如果有疑问的联系我们吧,这是我们的联系方式。好,关于本次内容就介绍到这里,谢谢。
255数据分析李博士 00:20查看AI文稿AI文稿
00:20查看AI文稿AI文稿今天教你做方叉分析,第一步,导入数据选择分析方法,方叉分析第二步,拖转样本查看结果,分析结果超清晰,可以导出多种格式,还可以复制表格,调整图表样式。智能分析分析建议,帮助你进一步完善方叉分析。你学会了吗?如有其他疑问,请在评论区告诉我。
75SPSSAU 00:32查看AI文稿AI文稿
00:32查看AI文稿AI文稿做方差分析一定要搞懂这几个指标, f 值和批值。方差分析最终分析时,首先分析批值,如果此值小于零点零五,说明呈现出差异性,具体差异在对比平均值即可。如果批值大于零点零五,则说明没有差异性产生, f 值属于中间过程值。想要计算批值,一定要先计算 f 值。 婴儿 so 也将 f 直结果输出,用 so 做方叉分析,各类图表一应俱全,方叉分析结果可是画图形深入分析,向硬量指标表格方叉分析中间过程值,还有智能分析分析建议帮助你理解方叉分析,你学会了吗?如有其他疑问,请在评论区告诉我。
1143SPSSAU


